Overview
Learn the mathematics behind the Fibonacci numbers, the golden ratio, and their relationship to each other. These topics may not be taught as part of a typical math curriculum, but they contain many fascinating results that are still accessible to an advanced high school student.
The course culminates in an exploration of the Fibonacci numbers appearing unexpectedly in nature, such as the number of spirals in the head of a sunflower.
Download the lecture notes from the link
https://www.math.hkust.edu.hk/~machas/fibonacci.pdf
Watch the promotional video: https://youtu.be/VWXeDFyB1hc
Syllabus
- Fibonacci: It’s as easy as 1, 1, 2, 3
- We learn about the Fibonacci numbers, the golden ratio, and their relationship. We derive the celebrated Binet’s formula, which gives an explicit formula for the Fibonacci numbers in terms of powers of the golden ratio and its reciprocal. This formula can be used to calculate the nth Fibonacci number without having to sum the preceding terms in the sequence.
- Identities, sums and rectangles
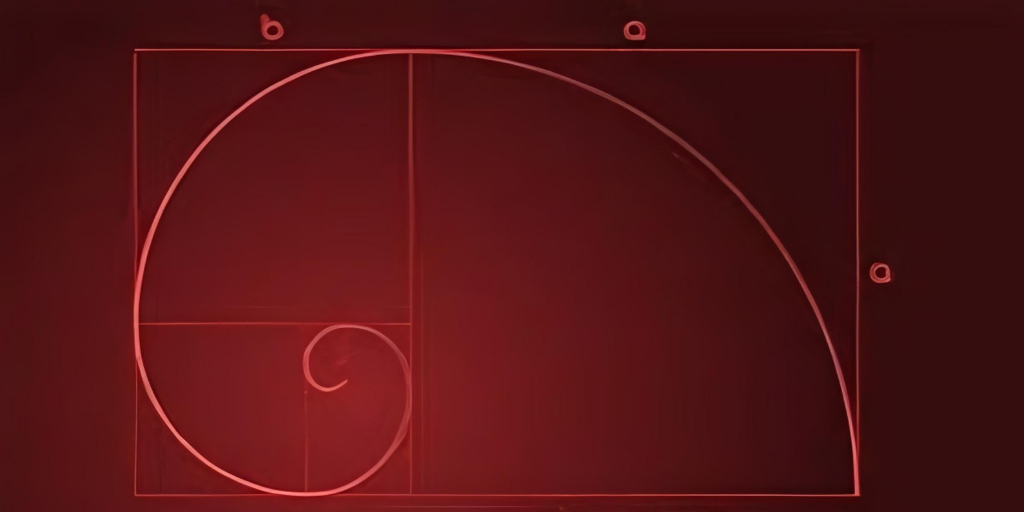
- We learn about the Fibonacci Q-matrix and Cassini’s identity. Cassini’s identity is the basis for the famous dissection fallacy, the Fibonacci bamboozlement. A dissection fallacy is an apparent paradox arising from two arrangements of different area from one set of puzzle pieces. We also derive formulas for the sum of the first n Fibonacci numbers, and the sum of the first n Fibonacci numbers squared. Finally, we show how to construct a golden rectangle, and how this leads to the beautiful image of spiraling squares. This image is a drawing of a sequence of squares, each with side lengths equal to the golden ratio conjugate raised to an integer power, creating a visually appealing and mathematically intriguing pattern.
- The most irrational number
- We learn about the golden spiral and the Fibonacci spiral. Because of the relationship between the Fibonacci numbers and the golden ratio, the Fibonacci spiral eventually converges to the golden spiral. You will recognize the Fibonacci spiral because it is the icon of our course. We next learn about continued fractions. To construct a continued fraction is to construct a sequence of rational numbers that converges to a target irrational number. The golden ratio is the irrational number whose continued fraction converges the slowest. We say that the golden ratio is the irrational number that is the most difficult to approximate by a rational number, or that the golden ratio is the most irrational of the irrational numbers. We then define the golden angle, which is related to the golden ratio, and use it to model the growth of a sunflower head. The use of the golden angle in the model allows a fine packing of the florets, and results in the unexpected appearance of the Fibonacci numbers in the sunflower.